Funkcje liniowe i kwadratowe to podstawa matematyki w szkole średniej i jeden z działów, które prawie zawsze pojawiają się na maturze. Dobra wiadomość? Można je świetnie zrozumieć i zapamiętać, jeśli potraktujemy je jak… opis codziennych sytuacji.
W tym wpisie pokażę Ci funkcje krok po kroku – z prostymi przykładami, które mają sens w realnym życiu.
🔹 1. Co to w ogóle jest funkcja?
👉 Funkcja to taki „automat do liczb”.
- Wkładasz liczbę (argument, np. x),
- Automat wykonuje działanie,
- Wychodzi wynik (wartość funkcji, np. f(x)).
Przykład codzienny:
Kupiłeś bilet autobusowy za 4 zł. Jeśli chcesz kupić x biletów, to zapłacisz:
f(x)=4x
Czyli dla 1 biletu → 4 zł, dla 5 biletów → 20 zł.
🔹 2. Funkcja liniowa – prostota w działaniu
Wzór ogólny:
f(x)=ax+b
- a → współczynnik kierunkowy (określa nachylenie prostej),
- b → wyraz wolny (gdzie linia przecina oś Y).
🏠 Przykład z życia: rachunek za prąd
Opłata stała za licznik: 20 zł miesięcznie.
Każda 1 kWh kosztuje 0,80 zł.
Jeśli zużyjesz x kWh, to rachunek:
f(x)=0,8x+20
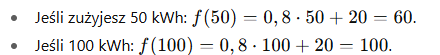
💡 Widzisz? To prosta linia rosnąca – im więcej zużywasz, tym więcej płacisz.
🔹 3. Funkcja kwadratowa – parabola w akcji
Wzór ogólny:
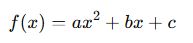
- Jeśli a>0 parabola „uśmiecha się” (ramiona w górę). 😊
- Jeśli a<0 parabola „smuci się” (ramiona w dół). ☹
⚽ Przykład z życia: lot piłki
Wyobraź sobie, że kopiesz piłkę. Jej tor lotu można opisać funkcją kwadratową:
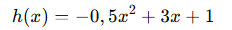

To właśnie parabola w praktyce!
🔹 4. Kluczowe elementy funkcji kwadratowej
🟢 Miejsce zerowe
To punkt, w którym wykres przecina oś X.
Liczymy ze wzoru:
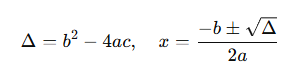
🟢 Wierzchołek paraboli
To punkt najwyższy lub najniższy.
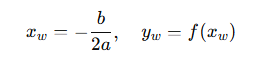
🟢 Symetria
Każda parabola jest symetryczna względem pionowej osi przechodzącej przez wierzchołek.
🔹 5. Jak odróżnić funkcję liniową od kwadratowej?
| Cecha | Funkcja liniowa | Funkcja kwadratowa |
| Wzór | f(x)=ax+b | f(x)=ax2+bx+c |
| Wykres | prosta | parabola |
| Przykład z życia | rachunek za prąd, koszty biletów | tor lotu piłki, most łukowy |
| Liczba miejsc zerowych | maksymalnie 1 | maksymalnie 2 |
🔹 6. Dlaczego warto je rozumieć?
➡️ Na maturze pojawiają się prawie zawsze – zarówno w wersji podstawowej, jak i rozszerzonej.
➡️ Funkcje to baza do wielu innych działów: nierówności, ciągi, trygonometria.
➡️ W życiu – spotykasz je wszędzie: ekonomia, fizyka, inżynieria, a nawet sport.
📌 Podsumowanie:
- Funkcja liniowa to prosta zależność typu „więcej → drożej”.
- Funkcja kwadratowa to parabola, którą łatwo zobaczyć w praktyce (np. lot piłki).
- Jeśli ogarniesz te dwa typy funkcji, zyskasz pewność na maturze – bo to pewniaki.
