Na maturze czas jest kluczowy. Znajomość wzorów to jedno, ale szybkie rozwiązywanie zadań wymaga też sprytnych trików i praktycznych metod. Poniżej znajdziesz 10 sprawdzonych technik, z przykładami i wzorami, które oszczędzą Ci czas.
1. Szybkie sprawdzanie podzielności
Zasada: nie trzeba dzielić całej liczby – wystarczy stosować reguły podzielności.
💡 Tip: przy zadaniach wielokrotnego wyboru możesz od razu odrzucić odpowiedzi, które nie spełniają tych warunków.
| Dzielnik | Zasada | Przykład |
|---|---|---|
| 2 | Ostatnia cyfra parzysta | 246 → ostatnia cyfra 6 → podzielna |
| 3 | Suma cyfr podzielna przez 3 | 123 → 1+2+3=6 → 6 podzielne przez 3 |
| 4 | Dwie ostatnie cyfry tworzą liczbę podzielną przez 4 | 1 236 → 36 ÷ 4 = 9 → podzielna |
| 5 | Ostatnia cyfra 0 lub 5 | 245 → podzielna |
| 6 | Podzielna przez 2 i 3 jednocześnie | 114 → 114 ÷ 2 = 57, 1+1+4=6 → podzielna przez 3 → podzielna przez 6 |
| 7 | Metoda „podwajania ostatniej cyfry” | 203 → 20 – 2×3 = 14 → 14 ÷ 7 = 2 → podzielna |
| 8 | Trzy ostatnie cyfry tworzą liczbę podzielną przez 8 | 1024 → 024 ÷ 8 = 3 → podzielna |
| 9 | Suma cyfr podzielna przez 9 | 729 → 7+2+9=18 → 18 ÷ 9 = 2 → podzielna |
| 10 | Ostatnia cyfra 0 | 1230 → podzielna |
2. Skrócone mnożenie i faktoryzacja
Znajomość wzorów skróconego mnożenia pozwala szybko upraszczać wyrażenia:
💡 Tip: dzięki temu unikniesz liczenia całych kwadratów w głowie.
3. Ułamki – zamiana w procenty
Zadania procentowe często występują w arkuszach maturalnych. Warto pamiętać szybkie przeliczenia:
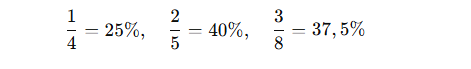
Przykład:
Zadanie: „Cena 80 zł wzrosła o 25%. Jaka jest nowa cena?” 80 ⋅ 1,25 = 100 zł
💡 Tip: zapamiętaj kilka podstawowych ułamków → zaoszczędzisz czas przy zadaniach tekstowych.
4. Obliczenia procentowe w kilku krokach

5. Szybkie sumy i różnice
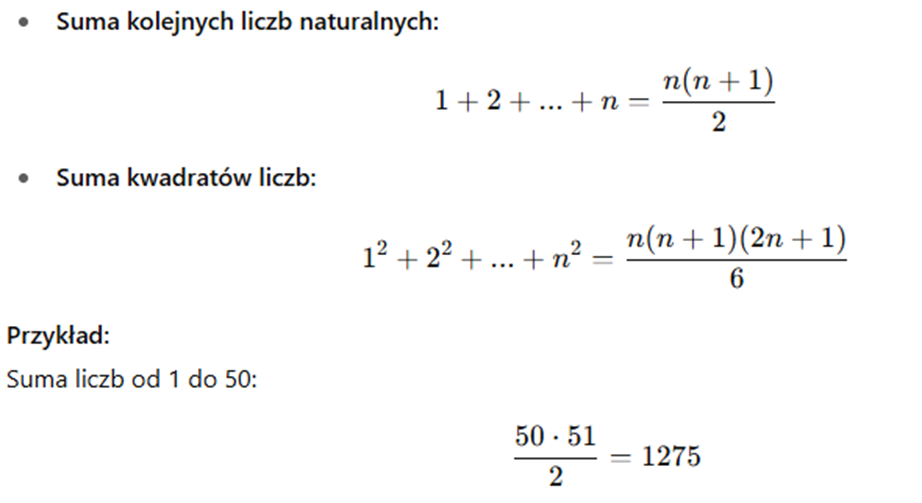
💡 Tip: przy zadaniach z ciągami liczbowymi użyj wzorów zamiast liczyć ręcznie.
6. Skrócone obliczenia średnich
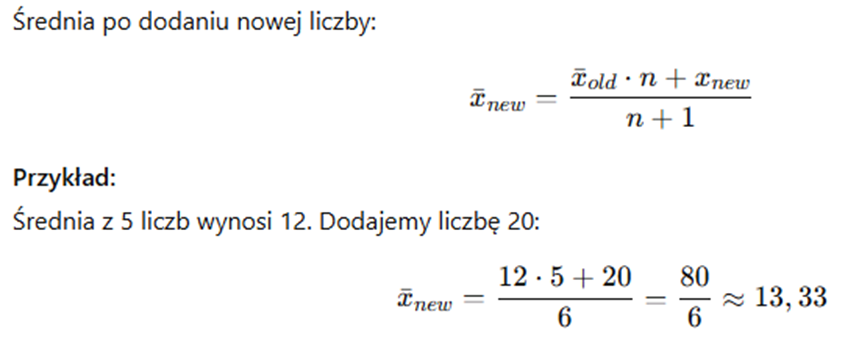
💡 Tip: szybko obliczysz średnią bez liczenia wszystkich liczb od nowa.
7. Geometria – skróty

8. Analiza zadania tekstowego
Trik: zamień tekst na równania krok po kroku:
Przykład: „Piotr ma 3 razy więcej jabłek niż Ania. Razem mają 48 jabłek. Ile ma Ania?”
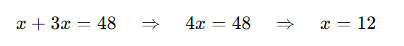
💡 Tip: rysunek lub schemat pomaga szybko zrozumieć relacje.
9. Zdarzenia i prawdopodobieństwo
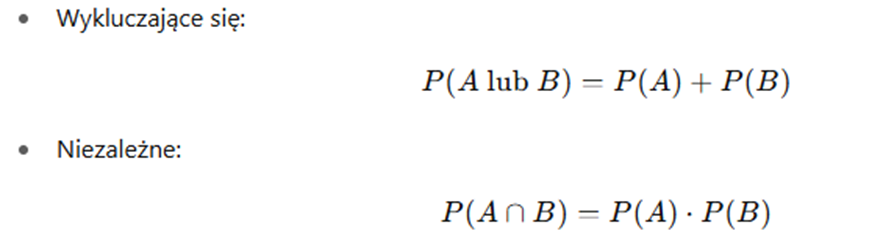
Przykład:
Rzut monetą i kostką:
- Prawdopodobieństwo, że wypadnie orzeł i 6 na kostce:
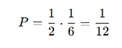
10. Skróty przy dużych liczbach
- Faktoryzacja i grupowanie wyrazów
- Szybkie oszacowanie wyników → eliminacja nierealistycznych odpowiedzi w zadaniach wielokrotnego wyboru.
Przykład:
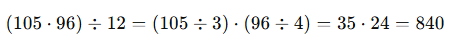
💡 Tip: umiejętność skrócenia obliczeń pozwala oszczędzić minuty na maturze.
